РАЗНОВИДНОСТЬ МОДЕЛИ ДЖИЛСА-АТЕРТОНА НЕЛИНЕЙНОГО МАГНИТНОГО СЕРДЕЧНИКА

 

Современные интегрированные пакеты программ схемотехнического анализа ORCAD, DESIGN LAB, MICROCAP и др. позволяют моделировать гистерезисные свойства ферромагнитных сердечников при перемагничивании в переменном магнитном поле. Однако, информация о том, какая конкретно модель магнитного сердечника используется в программах серии MICROCAP в настоящее время отсутствует. Это затрудняет моделирование нелинейных катушек индуктивности с помощью указанного пакета программ.

Ссылки в [1] на модель SPICE Level 2 [2, 3] неправомерны хотя бы потому, что не совпадают списки параметров моделей. Так в модель MICROCAP входит параметр ALPHA (параметр эффективности поля — Mean Field Parameter), тогда как в модель PSPICE входит PACK— коэффициент заполнения сердечника обмоткой. Остальные параметры обеих моделей совпадают.

Моделирование поведения сердечников в MICROCAP и ORCAD c одинаковыми общими параметрами без учета отличающихся (ALPHA=0, PACK=1) приводило к настолько сильно отличающимся результатам, что не оставляло сомнений в том, что используемые модели различны.

Поиск сведений на эту тему показал, что существуют две разновидности классической модели Джилса-Атертона. Одна из них используется в программе SPICE и подробно описана в [2, 3].

Вторая, которая собственно и используется в программах семейства MICROCAP, вычисляется с использованием безгистерезисной кривой намагничивания M_А(Н), построенной на основе гиперболического котангенса:

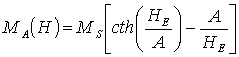,     ,             (1)

где M_S — намагниченность насыщения, A/м; Н — напряженность магнитного поля в сердечнике, А/м; A — параметр формы безгистерезисной кривой намагничивания; H_Е — эффективная напряженность магнитного поля в сердечнике, А/м; ALPHA — параметр эффективности поля, K — постоянная необратимой деформации доменных границ, С — постоянная упругой деформации доменных границ, d — знак изменения напряженности магнитного поля H.

Указанная модель сложнее, чем модель [2, 3], поскольку на каждом шаге интегрирования дифференциального уравнения перемагничивания

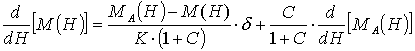,              (2)

приходится решать нелинейное алгебраическое уравнение (1).

Автором проведена серия расчетов петель гистерезиса для сердечников с различными модельными параметрами с помощью уравнений (1) и (2) с использованием программы MATCHCAD и программы схемотехнического анализа MICROCAP-7. Результаты сравнительных расчетов представлены на рис. 1.

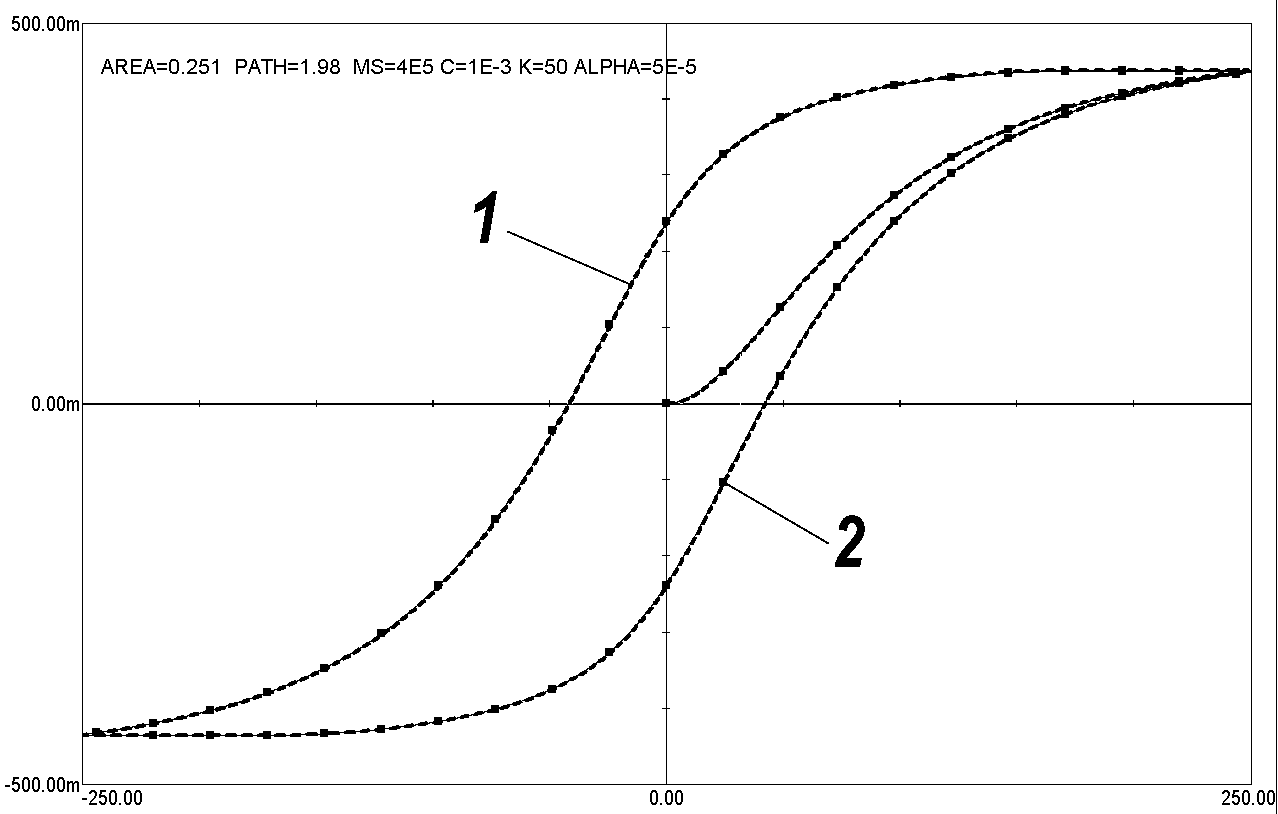
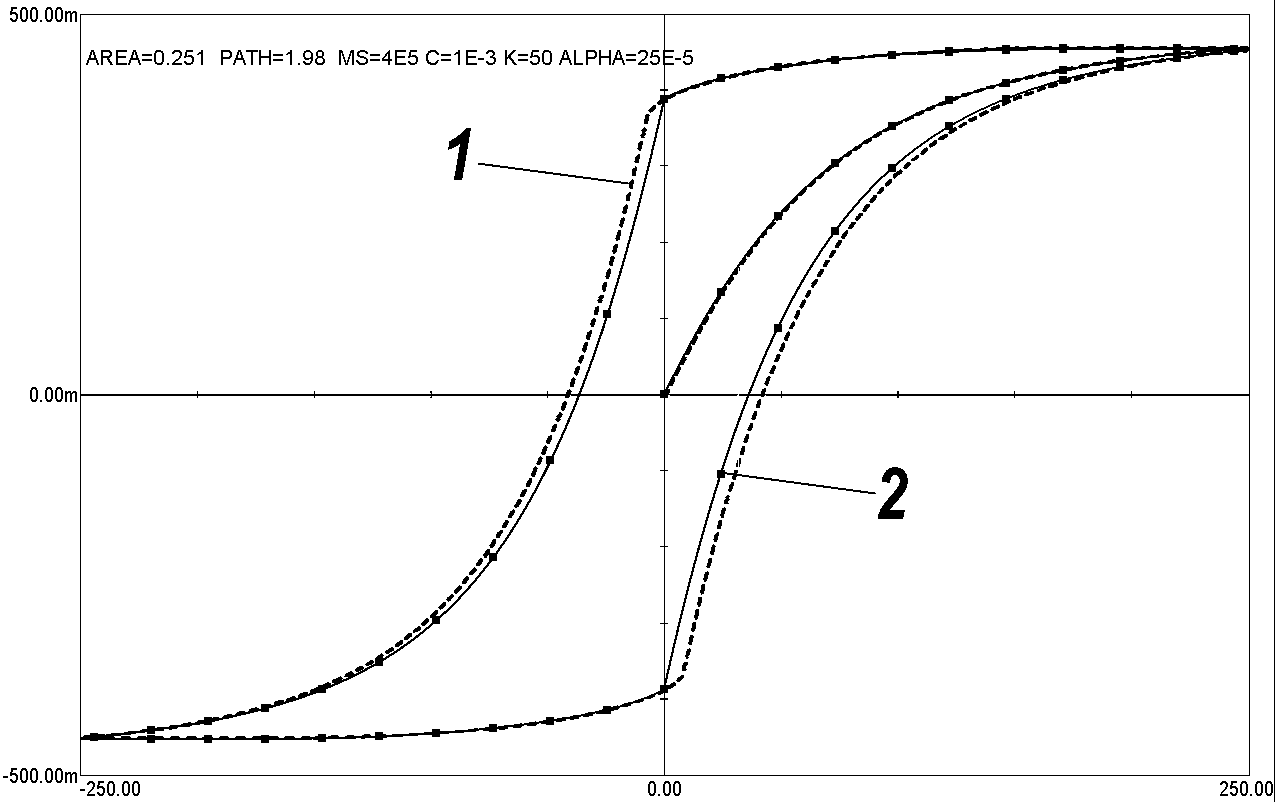
Рис. 1. Моделирование петли гистерезиса магнитного сердечника:  1 — в среде MATHCAD по уравнениям (1) и (2);   2 — в среде программы MICROCAP-7

Результаты расчетов в большинстве случаев полностью совпадают. Небольшое расхождение петель при увеличении ALPHA (см. рис. 1), объясняется погрешностью выбранного численного метода решения алгебраического уравнения (1) на каждом шаге интегрирования дифференциального уравнения (2).

Таким образом, серия сравнительных расчетов подтвердила предположение о том, что в пакете программ схемотехнического анализа MICROCAP используется разновидность модели Джилса-Атертона, в которой безгистерезисная кривая намагничивания строится согласно уравнению (1).

 

М.А. Амелина

ЛИТЕРАТУРА

1.   Разевиг В.Д. Схемотехническое моделирование с помощью Micro-CAP 7. — М.: Горячая линия–Телеком, 2003.

2.   Новиков А.А., Амелин С.А. Экспериментальное исследование параметров модели перемагничивания ферромагнетиков Джилса-Атертона //Электричество. 1995. N9. C. 46–51.

3.   Разевиг В.Д. Система сквозного проектирования электронных устройств Design Lab 8.0. – М.: «Солон», 2000.